이분탐색이란 ?
이분탐색은 정렬되어있는 리스트에서 탐색 범위를 반씩 좁혀가며 탐색하는 방식이다.
https://www.acmicpc.net/problem/1920
1920번: 수 찾기
첫째 줄에 자연수 N(1 ≤ N ≤ 100,000)이 주어진다. 다음 줄에는 N개의 정수 A[1], A[2], …, A[N]이 주어진다. 다음 줄에는 M(1 ≤ M ≤ 100,000)이 주어진다. 다음 줄에는 M개의 수들이 주어지는데, 이 수들
www.acmicpc.net
package codingtest;
import java.util.*;
import java.io.*;
public class Main{
static int N;
static int M;
static int[] A;
static int[] B;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
A = new int[N];
StringTokenizer st = new StringTokenizer(br.readLine());
for (int i=0; i<N; i++) {
A[i] = Integer.parseInt(st.nextToken());
}
Arrays.sort(A);
M = Integer.parseInt(br.readLine());
B = new int[M];
st = new StringTokenizer(br.readLine());
for (int i=0; i<M; i++) {
B[i] = Integer.parseInt(st.nextToken());
System.out.println(binarySearch(A,0,N-1,B[i]));
}
}
public static int binarySearch(int[] arr, int start, int end, int target) {
if (start>end) {
return 0;
}
int mid = (start+end)/2;
if (arr[mid]==target) return 1;
if (arr[mid]<target) {
return binarySearch(arr,mid+1,end,target);
}
return binarySearch(arr,start,mid-1,target);
}
}이분탐색을 활용하는 문제인 백준 1920번이다.
이분탐색을 활용하기 전에 Arrays.sort()로 탐색 대상 배열을 정렬해준다.
재귀를 활용해 이분 탐색을 구현했다.
찾고자 하는 값 target보다 arr[mid]가 더 크면 탐색 범위를 start ~ mid-1로,
arr[mid]가 더 작으면 탐색 범위를 mid+1~end로 좁혀나가며 탐색을 한다.
시간복잡도
[221220] 이분탐색과 시간복잡도
이분탐색이 무엇이고 시간복잡도는 어떻게 되며 그 이유는 무엇인가요?
velog.io
총 원소의 개수가 N개라면, 한번 탐색할 때 마다 N/2개로 감소한다.
k번 탐색한다면 남은 원소의 개수는 N*(1/2)^k 이다.
최악의 경우 N*(1/2)^k = 1 일때까지 탐색을 해야 한다.
위 식에서 양변에 2^k를 곱해주면 N = 2^k가 되고 양변에 log를 취해주면 logN = k가 된다.
즉 탐색 횟수 k는 logN이 된다. 따라서 O(logN)의 시간복잡도를 갖는다.
Upper bound와 Lower bound
이분탐색에서는 upper bound와 lower bound라는 개념이 있다.

lower bound는 왼쪽부터 볼 때 찾고자 하는 값(key) 이상의 값을 처음 만나는 위치이다.
즉 찾고자 하는 값인 4를 처음 만나는 인덱스인 3이 lower bound이다.
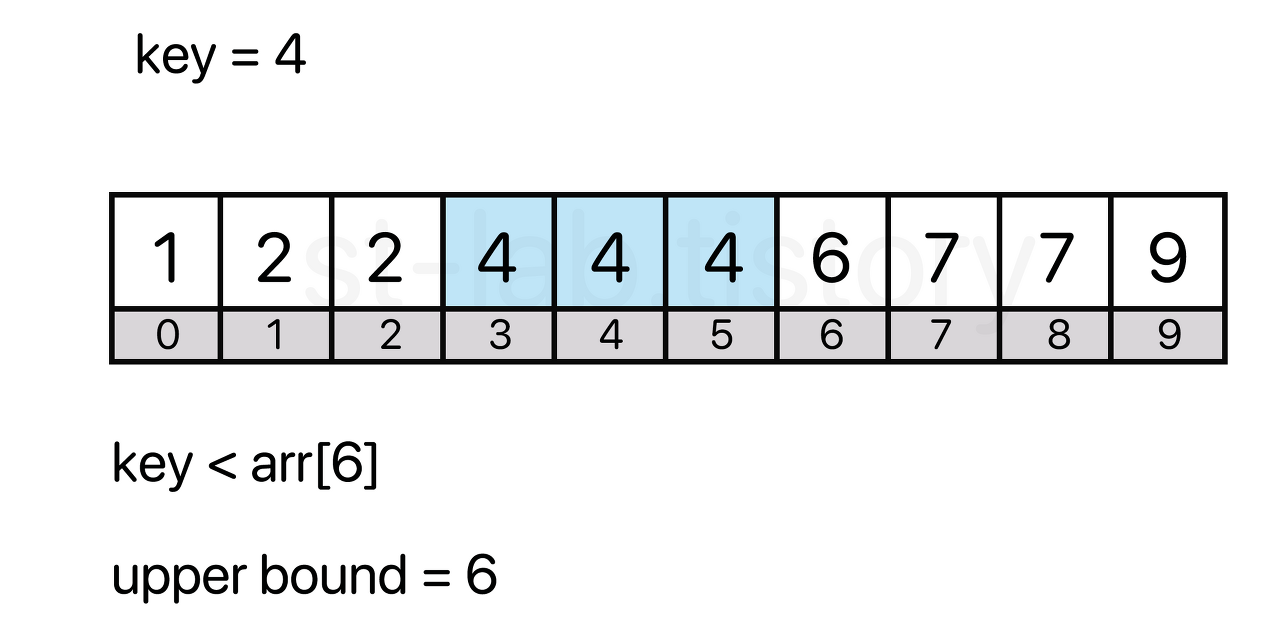
upper bound는 key값을 초과한 값을 처음 만나는 위치이다. 즉 위에서는 인덱스 6이다.

만약 찾고자 하는 값 (key=5)가 없다면? lower bound = upper bound = 6이 된다.
lower bound와 upper bound를 통해 중복 원소에 대한 구간의 길이 (upper bound-lower bound)를 알 수 있다.
https://yoongrammer.tistory.com/105
Lower bound & Upper bound 개념 및 구현
목차 Lower bound & Upper bound 개념 및 구현 Lower bound와 Upper bound는 경곗값을 찾는 알고리즘입니다. Lower bound와 Upper bound는 이진 탐색을 기반으로 하기 때문에 데이터가 정렬되어 있어야 합니다. 이진
yoongrammer.tistory.com
upper bound와 lower bound를 구하는 방법은 위 링크에 자세한 설명이 있다.
upper bound 구하는 방법
1. mid = (lo+hi)/2
2. mid와 key값 비교
if (mid<=key) : left = mid+1
else : hi = mid
3. lo>=hi 일때까지 반복
4. 반복이 끝나면 lo=hi 가 upper bound가 된다
lower bound 구하는 방법
1. mid = (lo+hi)/2
2. mid와 key값 비교
if (mid<key) : left = mid+1
else : hi = mid
3. lo>=hi 일때까지 반복
4. 반복이 끝나면 lo=hi 가 upper bound가 된다
결국 두 방법에서 차이는 2번에서 조건의 차이다
upper bound는 key 값을 넘는 최초 인덱스를 찾아야 한다.
띠라서 mid<=key 이면 lo = mid+1을 한다.
lower bound는 key 값인 최소 인덱스를 찾아야 한다.
따라서 mid>=key이면 hi=mid를 한다.
그리고 반복이 끝나는 시점에는 어차피 lo=hi가 되므로 둘 중 어느 값을 사용해도 상관이 없다.
https://www.acmicpc.net/problem/2110
2110번: 공유기 설치
첫째 줄에 집의 개수 N (2 ≤ N ≤ 200,000)과 공유기의 개수 C (2 ≤ C ≤ N)이 하나 이상의 빈 칸을 사이에 두고 주어진다. 둘째 줄부터 N개의 줄에는 집의 좌표를 나타내는 xi (0 ≤ xi ≤ 1,000,000,000)가
www.acmicpc.net
package codingtest;
import java.util.*;
import java.io.*;
public class Main{
static int N;
static int C;
static int[] arr;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
C = Integer.parseInt(st.nextToken());
arr = new int[N];
for (int i=0; i<N; i++) {
arr[i] = Integer.parseInt(br.readLine());
}
Arrays.sort(arr);
int lo = 1;
int hi = arr[N-1]-arr[0]+1;
while (lo<hi) {
int mid = (lo+hi)/2;
if (check(mid)) {
lo = mid+1;
} else {
hi = mid;
}
}
System.out.println(lo-1);
}
private static boolean check(int length) {
int now = 0;
int count = 1;
int distance = 0;
while (count<C) {
if (now==N-1) break;
distance += arr[now+1]-arr[now];
if (distance>=length) {
count+=1;
distance = 0;
}
now+=1;
}
if (count<C) return false;
return true;
}
}upper bound를 활용하는 문제다.
이분탐색 문제에서 핵심은 어떤 값을 대상으로 이분탐색을 할 지이다.
찾으려는 값을 대상으로 이분탐색을 해야 한다.
위 문제에서는 N개의 집에 C개의 공유기를 설치할 수 있는 집 사이의 최소 거리의 최댓값을 구해야 한다.
따라서 집 사이의 거리를 대상으로 이분탐색을 해야 한다.
그리고 집 사이의 최소 거리의 최댓값을 구하는 것이므로 upper bound를 활용해야 한다.
C개를 설치할 수 있는 집 사이의 최소 거리의 최댓값을 구해야 하므로 upper bound로 구한 뒤 1을 빼줘야 한다.
이분탐색을 진행할 대상을 정했으면 판단기준 (위 코드에서는 check())를 정해야 한다.
탐색한 값이 조건에 원하는 값보다 작은지, 큰지 판단하는 메서드로 역시 문제마다 다르게 구현한다.
위 문제 같은 경우 check 메서드에서 주어진 N개의 집에 C개의 공유기를 공유기 간 최소 거리의 최댓값이 현재 탐색 값이 되도록 설치할 수 있는지 판단한다.
false를 반환할 경우 최소 거리 간 최댓값이 구하려는 것보다 큰다. 따라서 거리를 줄여야 한다. hi = mid
true를 반환할 경우 최소 거리 간 최댓값이 구하려는 것보다 작다. 따라서 거리를 늘려야 한다. lo = mid+1
이분탐색을 활용한 upper bound, lower bound 문제는 대부분 위 문제와 비슷한 흐름으로 구성되는 것 같다.
이번에는 lower bound를 활용하는 문제다.
https://st-lab.tistory.com/281
[백준] 1300번 : K번째 수 - JAVA [자바]
https://www.acmicpc.net/problem/1300 1300번: K번째 수 세준이는 크기가 N×N인 배열 A를 만들었다. 배열에 들어있는 수 A[i][j] = i×j 이다. 이 수를 일차원 배열 B에 넣으면 B의 크기는 N×N이 된다. B를 오름차순
st-lab.tistory.com
참고한 풀이는 위 링크이다.
문제를 요약하면 N*N 행렬인 A를 1차원 행렬 B로 옮긴 후 오름차순 정렬했을 때 B[k]를 구하는 것이다.
A[i][j] = i*j이다.
B[k]=x라면 B에서 x보다 작거나 같은 원소의 개수는 최소 k개이다. (오름차순 정렬 했기때문)
최소 k개인 이유는 중복 원소가 있을 수 있기 때문이다.
그럼 이분탐색을 활용하려면
임의의 B[i]를 뽑고 B[i] 보다 작거나 같은 수가 i개이므로 i랑 k의 값을 비교해 이분탐색을 해야 한다.
탐색을 위해서는 lower bound를 써야 한다.
왜냐하면 B[k]=x인 k가 여러 개 있을 수 있다.
B[k]=x인 i가 여러 개 있을 때 upper bound를 쓰면 B 배열에서 x 다음 수인 어떤 수를 얻게 된다. 이 수를 통해 B[k]의 값을 알 수는없다.
lower bound를 쓰면 B 배열에서 B[k]=x인 첫번째 k를 찾게 되고 이것이 B[k] 값과 같기 때문에 이것을 활용하면 된다.
이것이 이분탐색이 사용되는 방법이다.
그리고 탐색 조건, 즉 B[i]=x일 때 x보다 작거나 같은 수의 개수를 찾는 방법이 필요하다.
이것은 행렬 A에서 i행은 i단이고, (i행은 1,2,3,4,5 .. , 2행은 2 4 6 8 10 ... )
각 단에서 x/i 한 값이 x보다 작거나 같은 수의 개수가 된다.
import java.util.*;
import java.io.*;
public class Main{
static int N;
static int k;
static int[][] arr;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
k = Integer.parseInt(br.readLine());
long lo = 1;
long hi = k;
while (lo<hi) {
long mid = (lo+hi)/2;
long count = 0;
for (int i=1; i<=N; i++) {
count += Math.min(mid/i,N);
}
if (k<=count) {
hi = mid;
}
else {
lo = mid+1;
}
}
System.out.println(lo);
}
}코드로 옮기면 위와 같다.
https://www.acmicpc.net/problem/12015
12015번: 가장 긴 증가하는 부분 수열 2
첫째 줄에 수열 A의 크기 N (1 ≤ N ≤ 1,000,000)이 주어진다. 둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (1 ≤ Ai ≤ 1,000,000)
www.acmicpc.net
위 문제도 lower bound를 사용하는 문제다.
가장 긴 증가하는 부분 수열, LIS를 구하는 방법을 알아야 한다.
방법은 단순하다.
현재 LIS의 끝 수보다 새로운 수가 크다면? LIS의 맨 뒤에 추가한다.
아닐 경우 LIS에서 새로운 수보다 큰 수 중 가장 작은 수를 새로운 수로 대치한다.
왜냐하면 이렇게 해야 앞의 수가 작아지고 최대한 증가하는 부분 수열을 만들 수 있기 때문이다.
그래서 대치하는 과정에서 이분탐색이 사용된다
이분탐색을 통해 LIS의 어떤 수를 새로운 수로 대치할 지 찾는 것이다.
import java.util.*;
import java.io.*;
public class Main{
public static void main(String[] args) throws IOException {
Scanner in = new Scanner(System.in);
int N = in.nextInt();
int[] seq = new int[N];
int[] LIS = new int[N];
for (int i=0; i<N; i++) {
seq[i] = in.nextInt();
}
LIS[0] = seq[0];
int lengthOfLIS = 1;
for (int i=1; i<N; i++) {
int key = seq[i];
if (LIS[lengthOfLIS-1]<key) {
lengthOfLIS++;
LIS[lengthOfLIS-1]=key;
}
else {
//lower bound 이분탐색
int lo = 0;
int hi = lengthOfLIS;
while (lo<hi) {
int mid = (lo+hi)/2;
if (LIS[mid]<key) {
lo = mid+1;
} else {
hi = mid;
}
}
LIS[lo]=key;
}
}
System.out.println(lengthOfLIS);
}
}
'알고리즘, 자료구조' 카테고리의 다른 글
| Dynamic Programming (0) | 2023.12.16 |
|---|---|
| 우선순위 큐 (0) | 2023.10.29 |
| 분할 정복 (1) | 2023.10.10 |
